Fit Multiple Data Sets

Fitting multiple (simulated) Gaussian data sets simultaneously.

All minimizers require the residual array to be one-dimensional. Therefore, in the objective we need to `flatten` the array before returning it.

TODO: this should be using the Model interface / built-in models!

import matplotlib.pyplot as plt
import numpy as np

from lmfit import Parameters, minimize, report_fit


def gauss(x, amp, cen, sigma):
    """Gaussian lineshape."""
    return amp * np.exp(-(x-cen)**2 / (2.*sigma**2))


def gauss_dataset(params, i, x):
    """Calculate Gaussian lineshape from parameters for data set."""
    amp = params['amp_%i' % (i+1)]
    cen = params['cen_%i' % (i+1)]
    sig = params['sig_%i' % (i+1)]
    return gauss(x, amp, cen, sig)


def objective(params, x, data):
    """Calculate total residual for fits of Gaussians to several data sets."""
    ndata, _ = data.shape
    resid = 0.0*data[:]

    # make residual per data set
    for i in range(ndata):
        resid[i, :] = data[i, :] - gauss_dataset(params, i, x)

    # now flatten this to a 1D array, as minimize() needs
    return resid.flatten()

Create five simulated Gaussian data sets

x = np.linspace(-1, 2, 151)
data = []
for i in np.arange(5):
    params = Parameters()
    amp = 0.60 + 9.50*np.random.rand()
    cen = -0.20 + 1.20*np.random.rand()
    sig = 0.25 + 0.03*np.random.rand()
    dat = gauss(x, amp, cen, sig) + np.random.normal(size=x.size, scale=0.1)
    data.append(dat)
data = np.array(data)

Create five sets of fitting parameters, one per data set

fit_params = Parameters()
for iy, y in enumerate(data):
    fit_params.add('amp_%i' % (iy+1), value=0.5, min=0.0, max=200)
    fit_params.add('cen_%i' % (iy+1), value=0.4, min=-2.0, max=2.0)
    fit_params.add('sig_%i' % (iy+1), value=0.3, min=0.01, max=3.0)

Constrain the values of sigma to be the same for all peaks by assigning sig_2, …, sig_5 to be equal to sig_1.

for iy in (2, 3, 4, 5):
    fit_params['sig_%i' % iy].expr = 'sig_1'

Run the global fit and show the fitting result

out = minimize(objective, fit_params, args=(x, data))
report_fit(out.params)

Out:

[[Variables]]
    amp_1:  6.35769745 +/- 0.02471391 (0.39%) (init = 0.5)
    cen_1: -0.06087255 +/- 0.00141148 (2.32%) (init = 0.4)
    sig_1:  0.27096733 +/- 6.7335e-04 (0.25%) (init = 0.3)
    amp_2:  6.23505243 +/- 0.02466565 (0.40%) (init = 0.5)
    cen_2:  0.90331537 +/- 0.00143924 (0.16%) (init = 0.4)
    sig_2:  0.27096733 +/- 6.7335e-04 (0.25%) == 'sig_1'
    amp_3:  6.74510330 +/- 0.02487197 (0.37%) (init = 0.5)
    cen_3:  0.30698606 +/- 0.00133040 (0.43%) (init = 0.4)
    sig_3:  0.27096733 +/- 6.7335e-04 (0.25%) == 'sig_1'
    amp_4:  3.62962270 +/- 0.02384778 (0.66%) (init = 0.5)
    cen_4:  0.00271542 +/- 0.00247235 (91.05%) (init = 0.4)
    sig_4:  0.27096733 +/- 6.7335e-04 (0.25%) == 'sig_1'
    amp_5:  6.29975266 +/- 0.02469084 (0.39%) (init = 0.5)
    cen_5: -0.15885172 +/- 0.00142452 (0.90%) (init = 0.4)
    sig_5:  0.27096733 +/- 6.7335e-04 (0.25%) == 'sig_1'
[[Correlations]] (unreported correlations are < 0.100)
    C(sig_1, amp_3) = -0.337
    C(amp_1, sig_1) = -0.320
    C(sig_1, amp_5) = -0.317
    C(sig_1, amp_2) = -0.314
    C(sig_1, amp_4) = -0.189
    C(amp_1, amp_3) =  0.108
    C(amp_3, amp_5) =  0.107
    C(amp_2, amp_3) =  0.106
    C(amp_1, amp_5) =  0.101
    C(amp_1, amp_2) =  0.100

Plot the data sets and fits

plt.figure()
for i in range(5):
    y_fit = gauss_dataset(out.params, i, x)
    plt.plot(x, data[i, :], 'o', x, y_fit, '-')
plt.show()

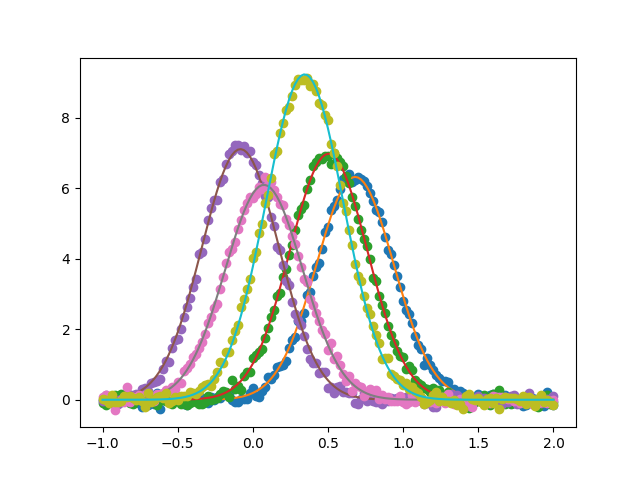
Out:

/Users/Newville/Codes/lmfit-py/examples/example_fit_multi_datasets.py:88: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()