Calculate Confidence Intervals

import matplotlib.pyplot as plt
from numpy import argsort, exp, linspace, pi, random, sign, sin, unique
from scipy.interpolate import interp1d

from lmfit import (Minimizer, Parameters, conf_interval, conf_interval2d,
                   report_ci, report_fit)

Define the residual function, specify “true” parameter values, and generate a synthetic data set with some noise:

def residual(pars, x, data=None):
    argu = (x*pars['decay'])**2
    shift = pars['shift']
    if abs(shift) > pi/2:
        shift = shift - sign(shift)*pi
    model = pars['amp']*sin(shift + x/pars['period']) * exp(-argu)
    if data is None:
        return model
    return model - data


p_true = Parameters()
p_true.add('amp', value=14.0)
p_true.add('period', value=5.33)
p_true.add('shift', value=0.123)
p_true.add('decay', value=0.010)

x = linspace(0.0, 250.0, 2500)
noise = random.normal(scale=0.7215, size=x.size)
data = residual(p_true, x) + noise

Create fitting parameters and set initial values:

fit_params = Parameters()
fit_params.add('amp', value=13.0)
fit_params.add('period', value=2)
fit_params.add('shift', value=0.0)
fit_params.add('decay', value=0.02)

Set-up the minimizer and perform the fit using leastsq algorithm, and show the report:

mini = Minimizer(residual, fit_params, fcn_args=(x,), fcn_kws={'data': data})
out = mini.leastsq()

fit = residual(out.params, x)
report_fit(out)

Out:

[[Fit Statistics]]
    # fitting method   = leastsq
    # function evals   = 90
    # data points      = 2500
    # variables        = 4
    chi-square         = 1212.08286
    reduced chi-square = 0.48561012
    Akaike info crit   = -1801.87620
    Bayesian info crit = -1778.58002
[[Variables]]
    amp:     13.9952862 +/- 0.04810194 (0.34%) (init = 13)
    period:  5.32947061 +/- 0.00267669 (0.05%) (init = 2)
    shift:   0.12201493 +/- 0.00472513 (3.87%) (init = 0)
    decay:   0.01002913 +/- 3.9913e-05 (0.40%) (init = 0.02)
[[Correlations]] (unreported correlations are < 0.100)
    C(period, shift) =  0.800
    C(amp, decay)    =  0.576

Calculate the confidence intervals for parameters and display the results:

ci, tr = conf_interval(mini, out, trace=True)

report_ci(ci)

names = out.params.keys()
i = 0
gs = plt.GridSpec(4, 4)
sx = {}
sy = {}
for fixed in names:
    j = 0
    for free in names:
        if j in sx and i in sy:
            ax = plt.subplot(gs[i, j], sharex=sx[j], sharey=sy[i])
        elif i in sy:
            ax = plt.subplot(gs[i, j], sharey=sy[i])
            sx[j] = ax
        elif j in sx:
            ax = plt.subplot(gs[i, j], sharex=sx[j])
            sy[i] = ax
        else:
            ax = plt.subplot(gs[i, j])
            sy[i] = ax
            sx[j] = ax
        if i < 3:
            plt.setp(ax.get_xticklabels(), visible=False)
        else:
            ax.set_xlabel(free)

        if j > 0:
            plt.setp(ax.get_yticklabels(), visible=False)
        else:
            ax.set_ylabel(fixed)

        res = tr[fixed]
        prob = res['prob']
        f = prob < 0.96

        x, y = res[free], res[fixed]
        ax.scatter(x[f], y[f], c=1-prob[f], s=200*(1-prob[f]+0.5))
        ax.autoscale(1, 1)
        j += 1
    i += 1

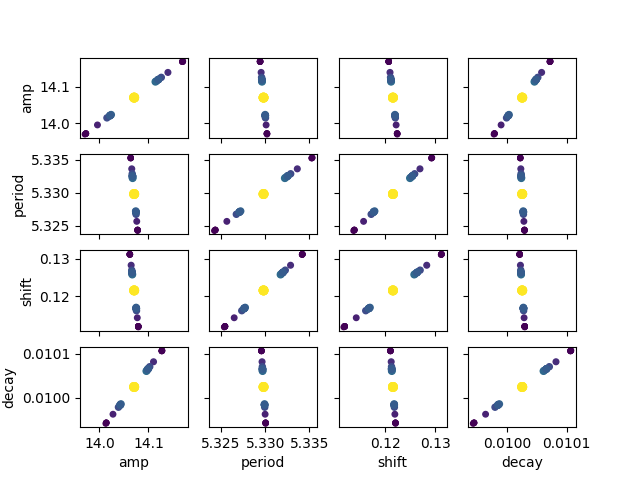
Out:

          99.73%    95.45%    68.27%    _BEST_    68.27%    95.45%    99.73%
amp   :  -0.14396  -0.09606  -0.04806  13.99529  +0.04794  +0.09637  +0.14466
period:  -0.00807  -0.00532  -0.00267   5.32947  +0.00267  +0.00534  +0.00811
shift :  -0.01420  -0.00947  -0.00473   0.12201  +0.00474  +0.00948  +0.01423
decay :  -0.00012  -0.00008  -0.00004   0.01003  +0.00004  +0.00008  +0.00012

It is also possible to calculate the confidence regions for two fixed parameters using the function conf_interval2d:

names = list(out.params.keys())

plt.figure()
cm = plt.cm.coolwarm
for i in range(4):
    for j in range(4):
        plt.subplot(4, 4, 16-j*4-i)
        if i != j:
            x, y, m = conf_interval2d(mini, out, names[i], names[j], 20, 20)
            plt.contourf(x, y, m, linspace(0, 1, 10), cmap=cm)
            plt.xlabel(names[i])
            plt.ylabel(names[j])

            x = tr[names[i]][names[i]]
            y = tr[names[i]][names[j]]
            pr = tr[names[i]]['prob']
            s = argsort(x)
            plt.scatter(x[s], y[s], c=pr[s], s=30, lw=1, cmap=cm)
        else:
            x = tr[names[i]][names[i]]
            y = tr[names[i]]['prob']

            t, s = unique(x, True)
            f = interp1d(t, y[s], 'slinear')
            xn = linspace(x.min(), x.max(), 50)
            plt.plot(xn, f(xn), 'g', lw=1)
            plt.xlabel(names[i])
            plt.ylabel('prob')

plt.show()

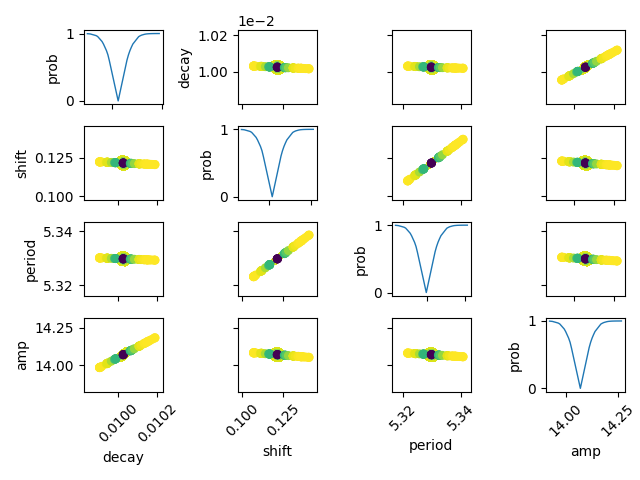
Out:

/Users/Newville/Codes/lmfit-py/examples/example_confidence_interval.py:135: UserWarning: Matplotlib is currently using agg, which is a non-GUI backend, so cannot show the figure.
  plt.show()