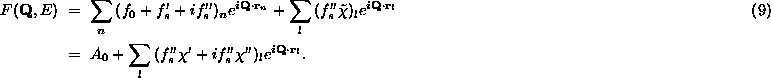
The kinematic diffraction intensity is proportional to the square of the structure factor,
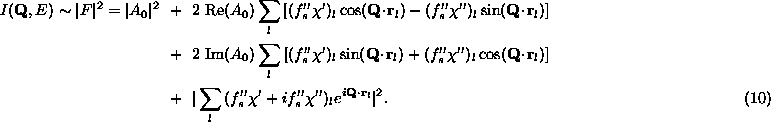
The first term,
To see how DAFS weights different crystallographically inequivalent sites,
it is helpful to separate the smooth atomic amplitudes for all the
atoms in the unit cell, labelled by n, from the fine structure terms for
just the resonantly scattering atoms, labelled by l, yielding
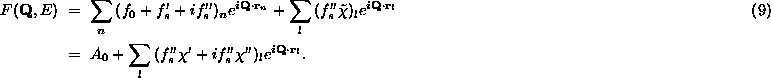
The kinematic diffraction intensity is proportional to the square of the
structure factor,
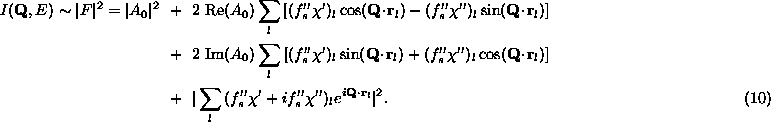
The first term, ![]() , represents the smooth atomic
contributions to the energy dependence of the Bragg intensities. The second
and third terms are the cross terms between
, represents the smooth atomic
contributions to the energy dependence of the Bragg intensities. The second
and third terms are the cross terms between ![]() and
and
![]() . The fourth term is the second order fine structure
contribution and is a smooth function versus photon energy.
. The fourth term is the second order fine structure
contribution and is a smooth function versus photon energy.
Because the leading order DAFS contributions to the intensity come from the
cross terms between ![]() and
and ![]() , the leading order
site-specific
, the leading order
site-specific ![]() and
and ![]() information appears linearly in the
Bragg intensities, and can be extracted using standard crystallographic
techniques. We can rewrite Eqn. 10 in terms of the
crystallographic weights
information appears linearly in the
Bragg intensities, and can be extracted using standard crystallographic
techniques. We can rewrite Eqn. 10 in terms of the
crystallographic weights ![]() ,
,
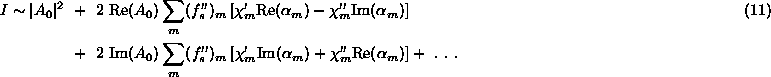
The site specific crystallographic weights depend on the diffraction
wavevector transfer ![]() and are given by the sum over all the
occurrences in the unit cell of each equivalent site, labelled by k,
producing one weight for each inequivalent site, labelled by m,
and are given by the sum over all the
occurrences in the unit cell of each equivalent site, labelled by k,
producing one weight for each inequivalent site, labelled by m,
![]()