The presence of oscillatory fine structure in the x-ray absorption spectra of atoms in solids has been known for over 70 years [1], and the analogous fine structure in x-ray diffraction has been known for almost 40 years [2]. It was not until intense synchrotron radiation sources became available, however, that the extended x-ray absorption fine structure technique (EXAFS) [3] became a routine spectroscopic method. In the last few years, with the development of modern multiple scattering MS-XAFS theory and analysis techniques, EXAFS has realized its potential as an accurate probe of distances and structure [4]. Recently, again because of synchrotron radiation sources, the diffraction anomalous fine structure technique (DAFS) has started to be used as a combined spectroscopic, structural, and crystallographic method [5, 6, 7, 8, 9, 10, 11]. Because the diffraction and absorption fine structures are closely related by unitarity and causality, the same sophisticated MS-XAFS techniques can be applied to DAFS measurements. This chapter describes the theoretical and experimental considerations behind DAFS, explains how DAFS measurements can be analyzed using unitarity and causality to relate and to isolate the real and imaginary components of the scattering amplitude, and illustrates how generalized MS-DAFS theory can be used to analyze the isolated diffraction fine structure.
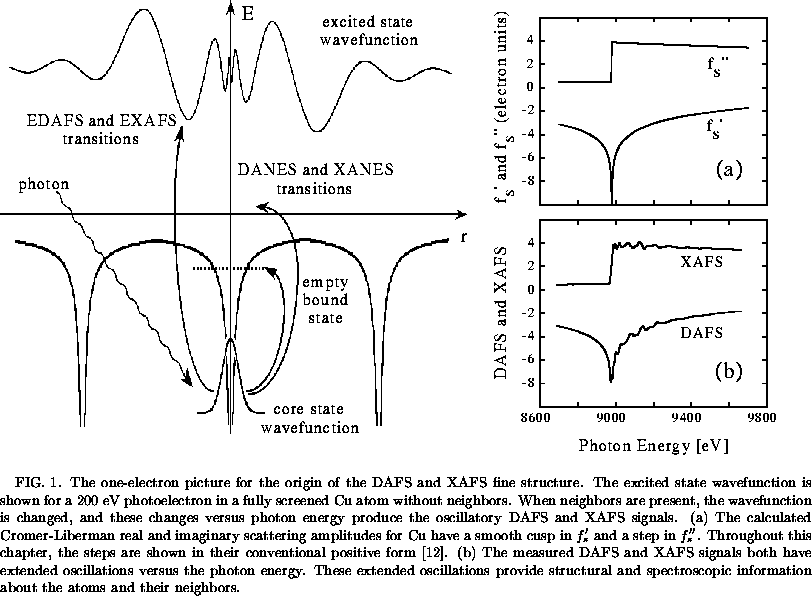
The common physical origin of DAFS and XAFS is illustrated schematically in Fig. 1.
In both DAFS and XAFS, the incoming photon promotes an electron from a
compact core state to an empty continuum state, or to an empty bound state.
When the electron is promoted to the continuum states at least 30 eV above
the edge, the absorption and diffraction oscillatory fine structure signals
are called EXAFS and EDAFS, respectively [3]. When the
electron is promoted to an empty bound state, or to the continuum states
below about 30 eV, the fine structure signals are called XANES and DANES
[3]. The intensity of the DAFS and XAFS signals for
each photon energy depends on the matrix elements between the ground state
wavefunction (the core state) and the excited state wavefunction. For the
EDAFS and EXAFS signals, the intensities depend on how well the excited
state wavefunctions fit into the ``effective boxes'' produced by the
central atom and the neighbors. For a simple box, these interference
effects would vary as 
, where the photoelectron
wavenumber 
depends on the difference
between the photon energy, E, and the electron binding energy, 
.
Note that the interference effects depend on the size of the box, which is
set by the bond length, 
, between the central atom and the neighboring
atom. Thus in this simple case, the oscillatory fine structure would
consist of a sum over all the neighbors, labeled by j, of terms. Because the walls of the ``real boxes'' are formed by the
screened excited central atom and by the surrounding atoms, there are
photoelectron wavenumber dependent phase shifts, 
, that slightly complicate the analysis. Fortunately, the
recent theoretical MS-XAFS advances have made it possible to calculate the
EDAFS and EXAFS signals precisely, and the full power of these techniques
can now be obtained routinely [4].
The physical origin of the causal relationship between the real and imaginary components of the forward scattering amplitude, and the connection between the forward dispersion relations and the analyticity of the scattering amplitude, are discussed very clearly by Toll [13].
Toll uses a proof by contradiction (see Fig. 2): Assume that a system could absorb some frequency components without disturbing any of the other frequency components, and consider the incoming Gaussian packet shown in Fig. 2a, which is composed of many different frequency components which extend over all time. Its central frequency components are shown in Fig. 2b. If the hypothetical system could absorb just these central components, with no change in the remaining components, then the output would be the original packet minus the absorbed components shown in Fig. 2c. This, however, would clearly violate causality because there would be an output before the incoming packet reaches the absorber. Therefore, the system cannot absorb some frequency components without phase shifting the remaining components to maintain zero output before the input arrives. Absorption and dispersion are intimately connected. Figure 2d shows the hypothetical output if the central frequency components are phase shifted by the imaginary component of the system's non-forward scattering amplitude, instead of being absorbed. Again this would clearly violate causality. At a fixed momentum transfer, the real and the imaginary components of the scattering amplitude are intimately connected. For each incoming and outgoing direction, the complex scattering amplitude is an analytic function of the energy. Consequently, the real and imaginary components of the scattering amplitude are related by Cauchy's theorem: they are a Kramers-Kronig or Hilbert transform pair.
The argument given above explains why the real and imaginary components of the scattering amplitude in any fixed direction are so closely related. To establish the connection between DAFS and XAFS, however, we need a relationship between the forward and non-forward amplitudes. The necessary connection comes from unitarity: To conserve probability, the incoming packet must be either transmitted, absorbed, scattered with a phase shift, or scattered without a phase shift. The optical theorem (a special case of unitarity) tells us that the sum of all the outgoing and absorbed waves must equal the incoming wave. For each photon energy, the optical theorem connects the angular integral of the elastic scattering (DAFS) over all directions to the absorption (XAFS). In general, this is the only connection. In the special case of pure dipole scattering, the scattering amplitude has the same energy dependence in all directions. Consequently, for pure dipole scattering the energy dependence of the imaginary component of the scattering amplitude is identical to that of the absorption, and the energy dependence of the real component is given by the Kramers-Kronig transform of the absorption. Because x-ray scattering is often predominantly dipolar, DAFS and XAFS can usually be related by angle independent Kramers-Kronig transforms.
