In non-relativistic quantum mechanics, neglecting the magnetic scattering
terms, the total atomic scattering amplitude, 
, for
photons with energy 
and with incident and scattered momenta
and 
, is the sum of the non-resonant Thomson
scattering amplitude, 
, and the ``anomalous'' scattering amplitude,
(see Fig. 3).
The Thompson and anomalous scattering amplitudes are given, in terms of the
classical single electron scattering amplitude, 
, by
[12, 14, 15, 16]
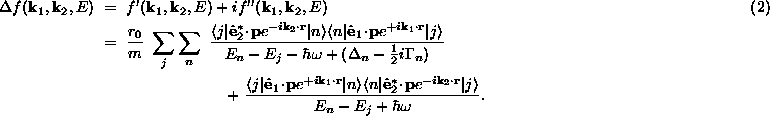
The self-energy corrections that produce the Lamb-shift 
and the linewidth 
of the
resonant term are shown explicitly [15].
The Thomson amplitude is a scalar which depends on the photon momentum
transfer, 
, and on the photon
polarization factors, 
, but is
independent of the photon energy. The Thomson amplitude is proportional to
the Fourier transform of the atom's electronic charge distribution. In
contrast, the anomalous amplitude depends separately on the incident and
scattered wavevectors, and , and also depends on the
photon energy, E. Thus, in general, is a tensor which
depends on the matrix elements between the ground state and the virtual
intermediate states, and is not proportional to the Fourier transform of
the total or subshell charge density [17]. It has been
established experimentally, however, that the and
dependencies of anomalous scattering are often small, and the full photon
energy- and momenta-dependent 
is
conventionally [14] approximated by its momenta-independent
forward scattering limit, denoted 
.
Consequently, the total atomic scattering amplitude, f, depends on the
photon energy, E, via its f' and f'' terms, and on the wavevector
transfer, 
, via its term.